Entropy is not “disorder”
Entropy change measures the dispersal of energy (at a specific temperature),
i.e. qrev/T
An introduction for instructors
Energy
of any type disperses from being localized to becoming spread out*, if
it is not constrained.
This is the ultimate basis of all statements about the second
law of thermodynamics and about all spontaneous physical or chemical processes.
* Energy
dispersal; energy becoming spread out.
In simple physico-chemical processes such as ideal
gas expansion into a vacuum , ”spread out” describes the literal
movement of energetic molecules throughout a greater volume than they occupied
before the process. The final result is that their initial , comparatively localized,
motional energy has become more dispersed in that final greater volume. . Such
a spontaneous volume change is fundamentally related to macro entropy change
by determining the reversible work (=-q) to compress the gas to its initial
volume, RT ln (V2/V1) with the result being ΔS
=R ln (V2/V1). On a molecular
thermodynamic basis, gas expansion into a vacuum would be described in
terms of microstates by the Boltzmann equation via:
ΔS = kB ln W2/W1
= kB ln [(V2 /V1 )N ]
= kBN ln V2 /V1
= R ln V2 /V1.
Thus, the amount of the spontaneous dispersion of molecules' energy in three-dimensional
space is related to molecular thermodynamics, to a larger number of microstates,
and measured by changes in entropy.
IMPORTANT NOTE: The initial statement above (about the movement of molecules into a larger volume as solely due to their motional energy) is only valid as a description of entropy change to high school students or non-scientists when there will not be any further discussion of entropy. Such a statement “smuggles in entropy change” wrote Norman C. Craig. I interpret this to be ‘smuggling’ because thermodynamic entropychange is not simply a matter of random molecular movement, but consists of two factors, not one. Entropy change is certainly enabled in chemistry by the motional energy of molecules (that can be can be increased by bond energy change in chemical reactions) but thermodynamic entropy is only actualized if the process itself (expansion, heating, mixing) makes accessible a larger number of microstates, a maximal Boltzmann probability at the specific temperature. [Information 'entropy' only has the latter factor
of probability (as does the 'sigma entropy' of physics, σ =
S/kB)
This clearly distinguishes both from thermodynamic entropy.]
Thus, to describe the cause of spontaneous events to less able or even to
many students, I see no harm in "smuggling in entropy" as appearing to be
simply a result of the nature of kinetic molecular behavior: Molecules spread
out or disperse in three-dimensional space IF they are provided with a greater
volume (and are separated from like molecules in a mixture). However, in speaking to capable students, the instructor should decide
how much to share with them. We ourselves, of course, must always be aware
that thermodynamic entropy involves the two factors of (1), motional energy
and (2), calculation that indicates how much that energy can be dispersed
(probability; the number of accessible microstates) under the conditions of the
process. Each is necessary; neither is sufficient alone.
• In the case of gas expansion both macro and molecular thermodynamic calculation procedures
can appear to be partly misleading to students and instructors so far as what
is happening in the system in regard to motional energy dispersal. In
macro thermodynamics, the restoration of the initial state certainly does
result in calculating -q, the amount of energy dispersed. However, volume appears to be the only variable — as it is, but only because it is the indication of how greatly molecular motional energy has been dispersed! Then, similarly, in molecular thermodynamics via statistical mechanics using a cell model (where one molecule occupies one cell), the only factor that changes is V, dependent on the number of additional unoccupied cells. However, each accessible cell represents not only a volume of space but a microstate containing a molecule with motional energy.. Therefore, although the final calculation appears to represent only V increase due to additional spatial “positions” , this is a misleading “smuggling in entropy change”. The essential enabling factor in thermodynamic entropy, molecular motional energy, is present (and should be mentioned to students) because it was explicitly in each accessible cell counted by the combinatorics of statistical mechanics.
• A microstate of a thermodynamic system is a state containing the total energy of the system in one of an extremely large number of accessible arrangements of the energy of each of its particles at one instant. The constant redistribution of that energy among the particles leads successively to other accessible arrangements. If the entropy of a system increases in some process or reaction, that means that there are more accessible microstates for that macro state. More microstates mean that there are more chances for the system's total energy to be in a different microstate at any time — in contrast to its lesser chances when fewer microstates are accessible (a relatively greater localization). That is the meaning in molecular thermodynamics of energy becoming “more spread out or dispersed”. (Energy becoming more “spread out” or “dispersed” does not mean something like “smeared over many microstates”, an impossibility. The expressions refer only to an increased number of accessible microstates in any one of which, at one instant, the total energy of the system might be. This increased number of microstates is the fundamental reason that the qualitative view of spontaneous “energy dispersal” is applicable to all types of spontaneous chemical processes — to three-dimensional space occupancy, to energy transfer to a cooler system, to formation of a mixture, or to a complex chemical reaction.)
A useful approach to microstates for students is here.
Entropy
change is measured by the dispersal of energy: how much is spread
out in a process, or how widely dispersed it becomes — always
at a specific temperature.
"energy" in
entropy considerations
refers to the motional energy of molecules, and (if applicable) any phase change,
and (in chemical reactions) bond energies in a system.
"dispersal
of energy" in macro thermodynamics occurs in two ways:
(1) "how much" involves heat transfer, usually ΔH, to or from system and thus from or to its surroundings;
(2) "how widely" means spreading out the initial energy of a system
in some manner, e.g., in gas expansion into a vacuum or mixing of ideal gases,
the system's volume increases and thereby the initial energy of any component is simply more dispersed in that larger three-dimensional volume without any
change in motional or other energies.
In chemical reactions, ΔG is the function that must be used
to evaluate the net energy dispersal in the universe of system and surroundings.
In macro thermodynamics, both spontaneous and non-spontaneous processes are ultimately
measured by their relationship to ΔS = qrev/T, where q is the
energy that is dispersible/dispersed.
In molecular thermodynamics,
all changes in the internal energy in a system or its surroundings
(either ΔH increase or decrease in a system, or any type of more
widely spreading its unchanged enthalpy) cause a change in the number of
microstates and thus an increase or decrease in entropy. (A microstate
is described above and also in detail at microstate.)
An entropy change that is measured by macro methods is related to W, the
number of microstates, by ΔS = kB ln
Wfinal /Winitial where
kB is the Boltzmann constant.
"motional energy", its meaning.
In my
writing for students, I sensed that many beginners are 'symbol challenged'
from dealing with the many 'deltas' of ΔH, ΔE, ΔU, PΔV, ΔT
(with ΔS and ΔG
now coming). Thus, I have used "motional energy" (that is due to molecular
motion)
to make less abstract
the ΔH involved in entropy change. Certainly, any instructor can
transmit to all levels of students the idea of energy dispersal in
entropy by "Molecules are astoundingly energetic particles. They average
over a thousand mph (near room temperature) in gases and liquids (and vibrating extremely rapidly
in solids) — colliding violently — and thus ceaselessly changing
their speeds, individual energy states and direction of movement. They're
instantly ready to bounce into any larger volume, if they aren't kept in
a crystal by the attraction of other particles — or, if a gas, obstructed
by a container (or a stopcock!) or if a liquid, kept from moving elsewhere
by the container." "Motional
energy" has dynamic connotations to better students that are implicit
in H or ΔH but may be too abstract to most beginners. In
chemistry, it is the kinetic energy of particles that in most simple processes
enables a system's energy in changing
from localized to becoming more dispersed or spread out.
The
other common source of change is in a chemical reaction where the enthalpies
of formation of the reactants are less than those of products that can
be formed from them.
In general terms, as an exothermic reaction is occurring, the -ΔH
of the process is first spread among the products, increasing their motional
energy, and then dispersed to the surroundings as the motion of the products
decreases to the temperature of the original system. In an endothermic
reaction, the required thermal energy is supplied to the system from (even
slightly) hotter surroundings. There is a fundamental difference between
the overall process of energy transfer in an endothermic reaction and simple
contact of a hotter system with one that is cooler.
(See the following section that treats such spontaneous heat transfer,
i.e., phase change.) In an endothermic reaction, the large
quantities of energy, equal to the ΔH
of the reaction, flow spontaneously from the surroundings because the temperature
of the system does not rise to that of the surroundings until "completion" of
the reaction. (“Completion” is in quotes because, of course, the final state may consist of an equilibrium mixture of the products and reactants rather than pure products.) The cause of the continued flow is the greater net dispersal of energy that occurs in the system during the process than the decreased dispersion in the surroundings, i.e., many more ways (microstates) that are accessible for the system's energy.
"phase change energy"
"Phase
change energy" is a potential energy change in a system. Therefore, it is not
as easily described to students as motional energy and, of course, is not
pertinent to all entropy discussions, i.e., not to those in which no phase
change has occurred from 0 K to the temperature being considered, or in
the process at hand. However, the phrase encompasses the important process
of transforming "motional
energy" to potential energy. In a fusion or vaporization phase change occurring
at a temperature minutely above the equilibrium temperature for such a
change, ΔH from energetic molecules in the surroundings
(molecular motion in the surroundings) causes the reversible breaking of intermolecular
bonds and/or bond reorganization in the system. This influx of energy from
the surroundings, in molecular thermodynamics terms, enormously increases WFinal,
the number of accessible microstates for the system. Furthermore in fusion, because of bond cleavage the original total vibrational (“motional”) energy of the molecules in the crystal is transferred to the translational movement of molecules in the liquid. The liquid-phase molecules rapidly break their bonds with adjacent molecules and can move a minute distance while making new bonds with other molecules. This motion, though slight, is far greater than the prior “dancing at a point” in the crystal. In vaporization, the thousand-fold increase in volume that becomes possible when intermolecular bonds in the liquid are broken results in an immense increase in accessible microstates — closer energy levels in greater volume leading to far larger numbers of those accessible microstates. (Of course, this can be presented to lower level students as simply “the energy of the liquid at the boiling point becoming more spread out in the larger volume”.)
"always at a specific temperature"
"always at a specific temperature" means
inclusion of T in any quantitative treatment of entropy change, fundamentally
as Dq(rev)/T. It is 'silent' in
isothermal processes such as ideal gas expansion, but active as a denominator
in phase change, and when temperature changes in a chemical process.
(1) In "how much" irreversible processes such as heating a system,
where the reversible entropy change is measured by incremental steps: ΔS
= Cp 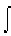 d
ln T and the energy, q(rev), that is dispersed reversibly stepwise to the
system from the surroundings (or the converse), is Cp dT.
d
ln T and the energy, q(rev), that is dispersed reversibly stepwise to the
system from the surroundings (or the converse), is Cp dT.
(2) In "how widely dispersed" irreversible processes such as gas
expansion into a vacuum, the reversible re-compression of the gas is ΔS
= -q(rev)/T = R ln [V2 /V1 ] and the "wider dispersal" of
the energy in the original expansion is RT ln [V2 /V1 ];
similarly, for fluids that mix to result in a combined volume, V2 ,
so that each component's internal energy that was originally confined in
a volume of VA or VB, becomes more widely dispersed: ΔS
= R ln [V2 /VA or B ], and the "wider dispersal" of
the component's energy is RT ln [V2 /VA or B ].
(3) In "how much AND how widely" reversible processes
such as phase change: ΔS = q(rev)/T where q(rev) is ΔH, the energy
dispersed to or from the system. Phase change is not an increase in the motional
energy of the system. It is an increase in the system's potential energy because
the heat transfer breaks intermolecular bonds — that will reform and release
the latent potential energy if the temperature falls below the phase change
equilibrium temperature. However, that bond-breaking also increases the number of locations accessible to molecules by allowing the vibrational energy of the crystal to be allocated to translation over greater distances in three dimensions. Thus, the description of "wider dispersal" of the original internal energy content by phase change is apropos. ("How much and how widely" also is an essential view of Chemical Reactions, as is developed in detail at the end of this presentation.)
As discussed before, with this terminology — and
knowingly "smuggling in entropy" — entropy change in gas expansion, for
example, can be
readily described to lower level classes simply as "What would energetic,
fast moving, continually colliding molecules of a gas do if they were in
a glass bulb and they were allowed to get into a bigger volume? Just sit
at the opening and stay in the bulb? Or spontaneously spread out their
thousand mile an hour motional energy all over that new larger volume?
Of course they'd zoom into a bigger space! That kind of spontaneous movement
by molecules, "spreading out their energy" (although involving no change
in temperature in ideal gases) is what
we call an entropy increase."
[As mentioned in the IMPORTANT NOTE in the box at the start of this web page,
probability and probability distributions are the very important second factor
in entropy change but for most students, this is a topic that can be saved
until physical chemistry.]
To
middle level students, the standard approach of describing gas expansion
into a vacuum can be used: Though there is no q or ΔH change in the
process,
a spontaneous event has occurred and thereby the innate "motional
energy" of the energetic molecules has become dispersed because the
process has given it space into which it can expand (the qualitative substitute
for the probability factor of entropy increase). Then, the ΔS in that
spontaneous process can be shown to be the negative of the reversible compression
to the original volume when calculated as ΔS
= q/T = R ln [V2 /V1].
To
the higher level students, the macro view of entropy change in gas expansion
caused by energetic molecules spreading out their energy in a larger volume
can be better related to molecular thermodynamics: That "motional energy" is "dispersed" in
the sense, first, of a larger number of microstates for the larger volume
as shown by the Boltzmann entropy equation, ΔS
= k ln [
W2/W1 ]
= k ln [ V2/V1 ]N = R ln [V2 /V1 ].
(Each fast-moving molecule can be thought of as occupying a tiny cell of volume
V1 . Then, if the volume of the system increases by the addition of an empty cell (doubling the volume available) , the energy of that molecule can be in two volumes (or, grossly speaking has been spread out in the larger volume of 2V1, even though this fact/emphasis has traditionally been hidden by the concept of "positional" entropy). But there are N molecules in a molar system,
so the [W2/W1] in the Boltzmann equation
becomes [2V1/V1]N Then, of course, the total
system energy after the expansion has the chance of being in any one of the
greater number of microstates at one instant than with fewer microstates before
the expansion. (As an alternate and more visual quantum mechanical approach
using energy levels for the total unchanged molecular energy, the relationship
of a particle in a 'one-dimensional
box' to the more closely spaced ("denser") energy levels in larger and larger
boxes can be developed. Thus, the additional accessible energy levels in larger
boxes can be described as leading to a great increase in the number of microstates
for the system, an increase in W2 — i.e., an increase in entropy
with increased volume.)
The meaning of ‘microstates’
(described near the start of this page and discussed in details here) can be briefly introduced as
follows:
If a
Figure of the changes in speed distribution in a gas with temperature has
appeared in the text (or can be drawn/projected for a class), it is easy
to show students qualitatively that heating a system causes its energy to
be far more dispersed.
The curves for the speeds in a hot gas are obviously broader, less centered
around fewer speeds, and thus both speeds and kinetic/motional energies (= mv2/2)
are more spread out than in a cooler gas. The original molecules have greater
and more different energies than before heating from simple considerations of
kinetic molecular theory. For a more advanced class, that increase in energy
due to heat input and the resulting change in the Figure can be said to result
in a greater number of microstates, W2 for the hotter system. Therefore,
there are more accessible microstates in any one of which the system might be
at any instant — the molecular
meaning of greater dispersal of the total energy (the original energy of
the system plus the added ΔHinput). entropysite.com contains an alternative verbal introduction to microstates here.
Thermal
energy always spontaneously flows from a hotter system (or subsystem)
to cooler surroundings (or subsystem), and conversely.
Such "hotter
to cooler" spontaneous transfers of energy are due to the nature of energy
to become more dispersed — if it is not constrained.
A
simple proof of the foregoing for beginning students could involve a hot
metal bar touching a bar that is just barely cooler. Designate q for the
thermal energy/"motional energy" in the solid metal
(actually 'vibrational energy, of course,
in the metal) that could be transferred between the bars under these
nearly reversible conditions, with T (bold type) for
the temperature of the hotter bar, and T for the temperature of the slightly
cooler. Therefore, because T is
larger than T, q/T is
smaller than q/T. If -q/T is
transferred from the hotter bar to the barely cooler bar, the cooler would
be given q/T. But q/T is larger than -q/T, so
the cooler bar has increased in entropy more than the hot bar has decreased.
Since the conditions are near reversibility (and the same entropy increase
would be found to be true at a larger temperature difference, via Cp 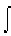 dT/T),
it can be generalized: Energy transfer from hot to cold systems results
in an increase in entropy. Then, because ΔS
= kB ln WFinal /WInitial ,
the number of accessible microstates in the cooler bar must have increased more than the number in the warmer bar decreased. The energy, q, hasn't changed but it is more dispersed in the cooler bar because there are more accessible microstates for the cooler bar in any one of which it (added to the original enthalpy of the system) might be at one instant. Thus, the entropy increase that we see in a spontaneous change is caused by increased energy dispersal.
dT/T),
it can be generalized: Energy transfer from hot to cold systems results
in an increase in entropy. Then, because ΔS
= kB ln WFinal /WInitial ,
the number of accessible microstates in the cooler bar must have increased more than the number in the warmer bar decreased. The energy, q, hasn't changed but it is more dispersed in the cooler bar because there are more accessible microstates for the cooler bar in any one of which it (added to the original enthalpy of the system) might be at one instant. Thus, the entropy increase that we see in a spontaneous change is caused by increased energy dispersal.
A
note on the global view of entropy change
Deciding
the direction of spontaneous change often involves considering a system
and its surroundings as a "universe". (This preceding case of two bars
of metal could be seen as such.) As a result, the global view (system plus
surroundings) of entropy change means examining the system and surroundings
together to find the net result of energy transfer, whether energy overall
has become more spread out and less localized. A difference in temperature
between a system and its surroundings is a prime case: Because energy always
becomes more dispersed in the cooler of the two than it was in the warmer,
such a transfer of energy is always spontaneous and the net result is a
greater entropy in the universe of system and surroundings. Entropy always
increases in the universe as a result of a spontaneous process
— one of the ancient expressions of the second law that is gibberish to the
average person and a major reason for stating it in the simpler terms of 'dispersal
of energy': "Energy of all types changes from being localized to becoming dispersed
or spread out, if it is not hindered."
Standard State Entropies,
So in Tables .
(An
So value is actually not "entropy", of course. It is an entropy change in
a substance because So is the result of the substance being
heated from 0 K to 298 K, a process that involved an incremental dispersal
of energy to the substance from the surroundings.)
My
early writing about the So of a substance described it poorly.*
It should have been "So is an index, relative to other substances,
of the ΔH energy
that has been
reversibly dispersed (at small temperature increments) to it from the surroundings to raise its temperature from 0 K to 298 K".
*The
word "at" in my original statement about So can be seriously
misunderstood, i.e., "a measure of the energy that can be dispersed within
the substance at T". The reversible energy transfer from the surroundings
to a substance that was carried out over the range of 0 K - 298 K can never
be thought to be effected at the single temperature T
of 298 K. That 298 K is the end of a long process from 0 K, not the temperature at
which any thermal energy was transferred!
In
considering So in terms of the amount of energy that has been
dispersed to a substance from its surroundings in the 0-298 K process,
it is best to use a word like "indicator" or "index" that less connotes "exact
numerical value" than does "measure" even though "measure" can have a general
and not a precise meaning. Thus, for example, that the So of
water is 69.9 joules/K-mol, in no way means that 69.9 joules have been
spread out/dispersed to a mole of water to heat it from 0 K and change
its phase from ice XI to ice 1H and then that ice to water! (Many many thousands of joules were involved in that process.) To determine
an entropy change (under reversible conditions) over a temperature range
from 0 K
is very complex
when the heat
capacity is radically changing, as described here:
Finding the entropy change in a substance from very low
temperatures up to 298 K is difficult, and not only because of experimental
problems at low temperatures.
The major problem is caused by the drastically varying heat capacity of
substances at low temperatures. In the calculations of entropy change with
temperature via the usual equation of ΔS =
Cp 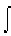 dT/T over a very wide range of temperatures above 250 K, the Cp can
be considered a constant with an error of only a few percent. In contrast,
from 15 K to 298 K, Cp values vary enormously — from <10 J/Kmol at
15 K to 75.3 J/Kmol for water at 298 K (and 139 J/Kmol for sulfuric acid,
with 217 J/Kmol for glycerol at 298 K). Therefore, the usual equation cannot
be used. Instead, a point by point plot of precise Cp /T values
vs. T is made and the area under the curve to 298 K is measured (equaling
the results of integration of an equation with a variable Cp ,
dT/T over a very wide range of temperatures above 250 K, the Cp can
be considered a constant with an error of only a few percent. In contrast,
from 15 K to 298 K, Cp values vary enormously — from <10 J/Kmol at
15 K to 75.3 J/Kmol for water at 298 K (and 139 J/Kmol for sulfuric acid,
with 217 J/Kmol for glycerol at 298 K). Therefore, the usual equation cannot
be used. Instead, a point by point plot of precise Cp /T values
vs. T is made and the area under the curve to 298 K is measured (equaling
the results of integration of an equation with a variable Cp ,
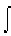 Cp /T
dT). Then, to this number (that is the result of "motional energy" transfer,
but is a complex function of T) is added the ΔH/T of any phase change
(including transitions from one crystalline form to another). In
addition, any 'residual entropy', determined from spectroscopic data, must
also be added. Thus, the final So is a cumulation of the reversible/stepwise
incremental entropy values from 0 to 298 K, a sum of the increase in motional
energy plus any phase change energy.
Cp /T
dT). Then, to this number (that is the result of "motional energy" transfer,
but is a complex function of T) is added the ΔH/T of any phase change
(including transitions from one crystalline form to another). In
addition, any 'residual entropy', determined from spectroscopic data, must
also be added. Thus, the final So is a cumulation of the reversible/stepwise
incremental entropy values from 0 to 298 K, a sum of the increase in motional
energy plus any phase change energy.
The
resultant summation in So , e.g. 69.9 joules/Kmol for water,
of course is not equivalent to the simple equation, ΔS
= qreversible or ΔHreversible /T, or
to any easy calculation of the amount of energy that has been dispersed
in the substance. (To repeat, So is
the result of a large number of reversible processes from 0 K to 298 K,
but itself not a reversible function at 298 K.) However,
any value of an So , e.g., 69.9 joules/K mol, is a
useful index, even though it may be much less than a hundredth or so of the energy
dispersed from the surroundings to a mol of substance from 0 K. It is extremely
helpful to view it as a roughly relative quantity
of energy that must be distributed in different substances/systems for
them to exist at 298 K . In fact, this considering of entropy in relative
terms of energy content or energy dispersal to a substance is a better
intuitive basis than entropy itself for the ordinary use of So in
general chemistry texts — namely, generalizing to link types of molecules
with their entropy values:
monatomic gases vs. polyatomic, congeneric elements of
increasing atomic weight, solids vs. similar solids in terms of the strength
of their bonds (K vs. Ca, KCl vs CaCl2), liquids vs. gases of
the same substance, diamond vs. graphite vs. metals vs. iodine, similar organic
compounds (or different types) of increasing molecular weight, compounds
vs. the hydrated compound etc., etc.
That
same fundamental difference, i.e., in the energy needed for substances
to exist at T, is implicit when general chemistry texts use entropy increases
to predict favorable conditions for reaction. (An increase in So of products
compared to reactants is commonly taken to mean an entropy increase in
the system - a favoring of the reaction as it is written. Basically, we
see that conclusion is due to the opportunity for greater dispersal of energy
in the products for their stable existence in the specified state at a particular
temperature.):
when a solid changes to a liquid, when a liquid changes
to a gas; when a mole of reactant forms two or mole moles of product – most
general when the products are gases, when the concentration of products compared
to reactants (measured by Q) is far less than at the equilibrium (measured
by the equilibrium constant, K).
Of
course, these rough predictions about the outcomes of chemical reactions
are superceded by the precise criterion for dispersible energy in both
surroundings and system, ΔG, and that for overall entropy increase, ΔG/T.
This will be discussed in detail later in connection with chemical reactions.
The Mixing of Ideal Liquids and of a Solute with a Solvent
Mixing of gases results in an increase in their volume and a greater density
of molecular motional energy levels — resulting in a large increase in the number of accessible
microstates for the final mixture. The same phenomena obviously cannot apply
to ideal liquids in which there is quite variable volume increase when they
are mixed. However, as has been said, "The `entropy of mixing' might
better be called the `entropy of dilution'". By this one could mean that the molecules of either constituent in the mixture become to some degree separated from one another and thus their energy levels become closer together by an amount determined by the amount of the other constituent that is added. It is not harmful to students that this approximate view be presented to them. Certainly, it is preferable to telling them that mixing is a different sort of entropy, “configurational” or “positional” entropy. The actual situation that is briefly stated below (and described in detail at calpoly_talk.html) is too complex for any but a few superior students, but it is essential to understanding entropy.
In general chemistry texts, configurational entropy is called 'positional
entropy' and is contrasted to the classic entropy of Clausius that is then
called 'thermal entropy'. The definition of Clausius of 'thermal energy'/T
is fundamental; positional entropy is derivative in that its conclusions
can be derived from thermal entropy concepts and procedures, but the reverse
is not possible. Most important is the fact that positional entropy
in texts — as is configurational entropy in statistical mechanics — usually
is treated as though the number of the positions of molecules in space determine
the entropy of the system. This is a valid probability calculation via combinatorics — and
the second factor in thermodynamic entropy, but traditionally this process
has been totally silent about any consideration of molecular energies of
the individual components that formed the solution. This is misleading. Those
molecular energies have not changed from their initial values, of course, but
their molecules (and their individual energies) have become literally more
dispersed, less localized in the final mixture). Any count of 'positions
in space' or of 'cells' in statistical mechanics implicitly includes the fact that molecules being
counted are particles with energy and so each cell is a microstate. Thermodynamic entropy
increase always involves an increase in energy dispersal at a specific temperature
no matter how the essential second factor of probability in thermodynamic
entropy is calculated or determined.
Colligative properties: The Effects of Entropy
Change in a Solution.
The fundamental basis for colligative effects is
that a solvent in a solution has a higher entropy than the pure solvent.
Obviously, the increase in entropy of the solvent is proportional to the
number of molecules of solute that may be added to it.
Freezing
of a liquid is a spontaneous process at any temperature that is infinitesimally
below the temperature at which a liquid and its solid and their surroundings
are in thermal equilibrium. There, because the surroundings of the liquid
are barely cold enough to reduce the liquid's molecular motion appropriately,
intermolecular bonds can form to yield a solid because the latent potential
enthalpy of fusion (stored in the liquid, measured as entropy) can reversibly
be dispersed to the surroundings.
However, the solvent in a solution has higher entropy
than pure solvent and this state of more dispersed motional energy does not
permit intermolecular bonds to form at the usual freezing temperature. (Traditionally
stated: The solvent's "escaping tendency" from a solution to form a solid
is less than from the pure solvent itself. ) The solvent in a solution cannot
freeze until its greater energy dispersal is decreased — visually,
conceptually, the molecules in motion are too spread out; molec thermodynamically,
there are too many microstates in any one of which the total energy of the
system might be — and so somehow the motion of the molecules should
be decreased. This can easily be done by cooling the solution, i.e. by lowering
the temperature of the surroundings. Then, because liquid water at 273 K,
as well as dilute solutions, have about twice the heat capacity (that is
actually an "energy
per degree" or "specific entropy") of ice or air a little cooling of the
solution decreases the motional energy of its molecules faster than the vibrational
energy of the ice decreases. As a result, at a degree or two below the normal
freezing point, an aqueous solution has had its entropy reduced enough to
be in equilibrium with its surroundings and thus able to release the latent
potential energy of bond formation reversibly and form ice.
Similarly, the solution will have a higher boiling point
than the pure solvent because solvent molecules, with their lesser escaping tendency,
require a higher temperature to raise their vapor pressure to reach an equilibrium
with the pressure of the surroundings.
Likewise, molecules of solvent on one side of a
semi-permeable membrane that has a solution on the other side will preferentially
go through the membrane to the solution. This occurs not solely for obvious
reasons of kinetics (although there is some preponderance of solvent molecules
at the membrane interface on the pure solvent side). The overriding effect
is due to the far greater tendency of the solvent molecules to spread out
their energy by leaving the pure solvent and going to the solution on the
other side of the membrane.
Chemical
Reactions — "how much" and "how widely" energy is dispersed.
The
Gibbs "free energy" equation: ΔG = ΔH - TΔS, an All-Entropy
Equation State.
Undoubtedly, the first-year chemistry texts that directly state the Gibbs
equation as
ΔG = ΔH - T ΔS, without
its derivation involving the entropy of the universe, do so in order to save
valuable page space. However, such an omission seriously weakens students'
understanding that the "free energy" of Gibbs
is more closely related to entropy than it is to energy. This quality of
being a very different variety of energy is seen most clearly if it is derived
as the result of a chemical reaction as is shown in some superior texts,
and developed below.
If there are no other events in the universe at a particular moment that
a spontaneous chemical reaction occurs in a system, the changes in entropy
are: ΔSuniverse = ΔSsurroundings + ΔSsystem.
However, the internal energy evolved from changes in bond energy, -ΔH,
in a spontaneous reaction in the system passes to the surroundings. This
- ΔHsystem, divided by T, is ΔSsurroundings.
Inserting this result (of - (ΔH/T)system = ΔSsurroundings) in
the original equation results in ΔSuniverse = - (ΔH/T)system
+ ΔSsystem. But, the only
increase in entropy that occurred in the universe initially was the dispersal
of differences in bond energies as a result of a spontaneous chemical reaction
in the system. To that dispersed, evolved bond energy (that therefore has
a negative sign), we can arbitrarily assign any symbol we wish, say - ΔG
in honor of Gibbs, which, divided by T becomes ( - ΔG/T)system. Inserted
in the original equation as a replacement for ΔSuniverse (because it
represents the total change in entropy in the universe at that instant):
- (ΔG/T)system
= -(ΔH/T)system + ΔSsystem. Finally, multiplying the whole by
-T, we obtain the familiar Gibbs equation, ΔG = ΔH - TΔS,
all terms referring to what happened or could happen in the system.
The "free energy, - ΔG, is not a true energy in the sense that it is not conserved
as energy must be. Explicitly ascribed in the derivation of the preceding paragraph
(or implicitly in similar derivations), - ΔG is plainly the quantity of energy
that can be dispersed to the universe, the kind of entity always associated
with entropy increase, and not simply energy in one of its many forms. Therefore,
it is not difficult to see that ΔG is indeed not a true energy. Instead, as
dispersible energy, when divided by T, ΔG/T is an entropy function — the
total entropy change associated with a reaction, not simply the entropy change
in a reaction, i.e., Sproducts - Sreactants, that is the ΔSsystem. This is why ΔG
has enormous power and generality of application, from prediction of the direction
of a chemical reaction, to prediction of the maximum useful work that can be
obtained from it. The Planck function, - ΔG/T, is superior in characterizing
the temperature dependence of the spontaneity of chemical reactions . These
advantages are the result of the strength of the whole concept of entropy itself
and the relation of ΔG to it, not a result of ΔG being some novel variant of
energy.
Relationship of ΔGo to ΔG
for Non-standard Conditions
Far more important practically than the foregoing
use of standard states in ΔGo = ΔHo - TΔSo — because
therein all constituents are assumed to be confined to the unreal world of 1M or 1 bar concentrations
— is a modification of that equation that can include differences in
realistic concentrations of the reactants and products. Many texts present
the result, ΔG
= ΔGo + RT ln Q, where Q is the reaction quotient after
only a brief discussion of a reaction attaining an equilibrium state. (A
notable exception is the careful development in General Chemistry, 8th edition,
by Petrucci, Harwood, and Herring.)
Even though this equation may not be developed in
detail in a text or a class, it certainly should be better explained to students
than it is in most texts. The inclusion of RT ln Q so that the equation becomes ΔG
= ΔGo + RT ln Q involves practical concentrations, but why does
it "work"? And, if the more detailed equation is shown ΔG = ΔHo - (TΔSo - RT
ln Q), why is that RT ln Q associated with the entropy part of the equation — how
can RT ln Q be a change in entropy?
Many good general chemistry texts have a preliminary
development of entropy changes that occur in dissolving ionic solids in water.
Some mention entropy increase when gases or liquids mix. (Chemistry, 2nd edition,
by Moore, Stanitski, and Jurs is unique in its thorough treatment of this
topic from the first mention of reactions in gases.) A simple explanation
of the RT ln Q "problem" would start with stating that mixtures of fluids
(gases or liquids) have an increased entropy than the pure gas or liquid
because the energy of each component is spread out in the final larger volume
for gases and the greater number of 'cells' for liquids.
Therefore, a mixture of some amount(s) of reactants with some amount(s) of
products has a higher entropy than any single pure product or mixture of products.
But a mixture of products and reactants that is an equilibrium mixture
as a result of a spontaneous change would have the largest entropy value
of any possible combination — by the very definition of equilibrium. An equilibrium
is a stable unchanging ratio of components because that ratio is the maximal
entropy for the particular system.
From the foregoing, it should be clear not only
why RT ln Q is part of a 'realistic' treatment of the Gibbs energy equation,
but also that as Q changes toward K, the equilibrium constant, during the
course of a reaction, and ends at K. A professor
in Minnesota
(who modestly wishes to
be unnamed) has written that "when a stoichiometric amount of reactants is
turned into products, ΔSuniverse =
R ln K/Q". I don't know
if this is common elsewhere in the literature, but I believe it to be unusually
significant - entropy
maximization in spontaneous events as complex as chemical reactions can be
expressed concisely. Spontaneous energy dispersal, the causal factor for
entropy increase, is as fundamental to the Gibbs energy equation as it is
in all energy-related chemical behavior.
entropy.lambert@gmail.com
Last revised and updated: November 2005
![]() d
ln T and the energy, q(rev), that is dispersed reversibly stepwise to the
system from the surroundings (or the converse), is Cp dT.
d
ln T and the energy, q(rev), that is dispersed reversibly stepwise to the
system from the surroundings (or the converse), is Cp dT.